1年生の数学で球の表面積について学びました。球の表面積を導き出す公式は「4πｒ²」ですが、そうなる理由を説明せよと言われると・・・。
　今日の授業の中で、実験でこの公式を体験していました。
①球を半分に切断したものの周りに、ロープを巻いていきます。（コマ回しの要領で。）


②このロープの厚み×長さ×２が球の表面積になります。


③このロープを球の半径と同じ長さの半径の円を底辺とする円柱にロープを巻き付けていきます。


④すると円柱の高さが円の直径と同じ場合、ちょうど真ん中までロープを巻き付けることができました。


⑤以上のことから、球の表面積＝同じ半径を持ち、円の直径と同じ高さを持つ円柱の側面積　となります。


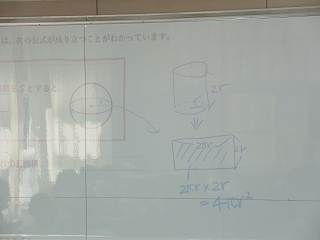
⑥円の半径をｒとすると円柱の側面積は、高さ（２ｒ）×円の周の長さ（２πｒ）なので、計算すると４πｒ²となるようです。


これを正しく証明しようとすると、高校の数学３で学ぶ知識を習得するまで待たなければいけないようですが、一見、無味乾燥なイメージを持ちがちな数学の公式も、実体のある実験の中で目の前に見られると興味もわき、知識としても定着できるのではないでしょうか？